相关连结:http://www.esstartek.com/yellowpage/product_cg146475.html
StartFromHere

远心镜头 设计目的就是消除由於被测物体(或CCD晶片)离镜头距离的远近不
一致,造成放大倍率不一样。根据远心镜头分类其设计原理如下:
1.物方远心光路设计原理及作用:
物方主光线平行於光轴主光线的会聚中心位於像方无限远,称之为:物方远心光路。其作用为:可以消除物方由於调焦不准确带来的,读数误差。
2.像方远心光路设计原理及作用:
像方主光线平行於光轴主光线的会聚中心位於物方无限远,称之为:像方远心光路。其作用为:可以消除像方调焦不准引入的测量误差。
3.两侧远心光路设计原理及作用:
综合了物方/像方远心的双重作用。主要用於视觉测量检测领域。
从以上各类远心镜头设计原理即可看出,远心镜头是在充分利用光学成像特性,充分考虑在成像中光线的影响而设计的高精度镜头,目前在机器视觉精密测量、高精度检测领域已被广泛应用。
EndAtHere
远心光学系统公司(ES)是一家专业的远心光学、视觉照明、机电产品研究、设计、开发、制造的高科技企业。满足客户对特殊规格和特性的需求,公司可量身为您定制远心光学镜头、视觉照明、远心光学系统设备平台等软硬体,并为您提供一站式技术顾问服务,使您更简单、更快速地建立自己的自动化远心视觉应用系统。
在产品选型中,有的朋友对於光学的专业术语或多或少会有一些疑问,今天,小编为您答疑解惑悉数奉上。
一、数值孔径N.A.:
当物件的入射光瞳时半形是u,而折射率是n,n*sin u是物体方数值孔径N.A.;
当物件的出射光瞳时半形是u',而折射率是n',n'*sin u'是物体方数值孔径N.A.;
数值孔径是一个度量镜头解析度及光亮度的重要指标,N.A.数值越高,解析度及光亮度越高。
二、解析度:
能清楚区分被测物体细微结构最小间隔的能力。即,能清楚区分相邻两个物点间最小距离的能力。解析度越大,两点之间可区分的最小距离越小。数值孔径越大,解析度越高。
解析度公式:解析度(ε)=0.61×λ/N.A.
λ:使用的波长或辐射(λ=0.55um用於可见光)
N.A.:物镜数值孔径
三、景深:
景深是指无需重新调焦即可保持可接受的图像清晰度的距离。
景深计算公式:
景深=2×(允许弥散圆×有效Fno/放大倍率2)=允许弥散圆/(N.A.×放大倍率)
(注:有效Fno=放大倍率/2N.A.)
四、F数/光圈数:
<显示了光亮度,计算方式是镜头焦距除以从镜头的物体测观测到有效直径(入射光瞳D mm)。它可以用N.A.及镜头的光学放大率(β)计算出来。Fno=f/D= β/(2×N.A.)。
五、有效F数/有效光圈:
有效F数显示了物体在有限距离的镜头光亮度。用来表示实际使用的镜头的光亮度数值,光学放大率越高,镜头越暗。有效Fno=(1+β)×Fno。
六、放大倍率:
电子放大倍率:用相机拍照成像呈现在显示器的放大倍率。
光学放大倍率(β):影像大小相对於物体的放大倍率。
β=影像/物体=N.A./N.A.'=CCD相机靶面尺寸/视场实际尺寸
有效F数显示了物体在有限距离的镜头光亮度。用来表示实际使用的镜头的光亮度数值,光学放大率越高,镜头越暗。有效Fno=(1+β)×Fno。
七、视场:
视场是镜头与CCD相机连接时物体可被看见的范围大小。
视场大小=(CCD靶面大小)/(光学放大倍率)。
八、焦距/后焦点/前焦点:
焦距:光学系统中心到焦点的距离;
后焦点:最后一片镜片到后侧焦点的距离;
前焦点:最前一片镜片到前侧焦点的距离。
远心光学(ES)核心技术人员在航太、军工领域从事光学设计、制造工作10多年,积累和掌握了一系列先进的远心光学、光机及视觉照明技术、制造工艺及严谨的测试流程。产品精良,在行业应用中获得诸多好评,有相关的行业知识您都可以在网站的技术资料中查阅。
在计量学应用中进行精密线性测量时,经常需要从物体标准正面观测,此外,许多机械零件并无法精确放置,测量时间距也在不断变化,而软体工程师却需要能够精确反映实物的图像。这就需要用远心镜头来完成--高远心度、无透视误差。
远心度是描述主光线偏离於光轴的角度,角度越小远心度越好,成像就越精确。一个理想的远心镜头没有梯形畸变,远心度是0°。
对於很多应用需要用到远心镜头是因为远心镜头在很大工作距离内的放大倍率接近恒定,消除了视角误差。这就意味著物体运动不会影响像的放大倍率。
需要注意地是:并不是远心镜头就比普通镜头有更大的景深。事实上,远心度高并不意味著景深大,景深仅仅依赖於F-number和解析度。使用远心镜头,随著物体远离最佳焦距成像也会模糊,但是它是对称模糊(这已被当作远心镜头的优点)。

普通镜头拍摄 双远心镜头拍摄
只要物体的特徵在远心镜头工作距离内,像的放大倍率保持恒定,换言之,即离透镜近的特徵并不比离的远的成像大。比如需要同时检测相隔10mm的两个相同螺丝的螺纹分布。
左图是普通镜头拍摄的,存在视角误差,放大倍率不一致;右图是我们ES Star的双远心镜头ESCM125-80-AL搭配远心光源拍摄,全视场无视差,拍摄画面很完美。
解析度(resolution)又称分辨力、鉴别率、鉴别力、分析力、解像力和分辨本领,是指摄影镜头清晰地再现被摄景物纤微细节的能力,是评价镜头品质的一个重要参数。显然解析度越高的镜头,所拍摄的影像越清晰细腻。它的优点是可以量化,用资料表示(图像解析度一般以量化图像感测器即空间频率对比度CTF(对比传递函数)来衡量),使结果更直观、更科学、更严密。
解析度定义为在像面处镜头在单位毫米内能够分辨开的黑白相间的条纹对数,如下图所示:

解析度为1/2d,其中,d为线宽。解析度的单位为lp/mm(线对/毫米)。
一般使用的解析度公式:
解析度(ε)=0.61×λ/N.A.(Reyleigh公式)
λ:使用的波长或辐射(λ=0.55µm用於可见光)
N.A.:物镜数值孔径
在实际工业应用中,系统使用面阵或线阵感测器作为成像器件,因此系统的解析度通常也会受到成像感测器中像元解析度的限制。像元解析度定义为单位毫米内图元单元数的一半,即=1/2P,其中p为图元单元的尺寸大小。例如一个CCD的像元尺寸大小为5×5微米,则像元解析度则为:=1/(2*0.005)=100(lp/mm)。感测器的像元解析度限制了系统的最高解析度,即使镜头的解析度再高,系统也不可能分辨高於像元解析度的细节。
在实际使用中,普通镜头解析度低,即使搭配高图元的相机,最后也只能生成模糊的影像。而采用我们BTOS远心光学公司的镜头,即使是配合小图元图像感测器,也能生成高解析度图像。

ES 远心镜头 普通镜头
景深,在光学摄影中是一个很重要参数,它的大小决定著清晰图像范围。在远心光学成像中,景深也是一个经常被提及的参数,它的大小取决於镜头倍率、光圈数、波长、图元大小、客户使用的边缘提取演算法灵敏度。对於大多数远心系列镜头,陈述的景深是在光圈数为8的整体景深。景深可用于测量应用,它通常比缺陷检测景深要大,图像的对比度必须尽可能高。
由於这个原因,远心光学系统(ES Stacy)公司的产品记录指出,"景深边界,图像可仍用於测量,但为了得到一个非常清晰的图像,应考虑只有一半的名义景深"。景深非常困难用参数来定义:它取决於倍率、光圈数、波长、图元大小、客户使用的边缘提取演算法的灵敏度。由於这个原因:没有客观的,也没有标准的方式来定义它:这是一个主观参数。
一个简单的法则,快速计算景深的方法如下:
景深 = (工作光圈数 * 图元大小 * 应用程式特定参数) / (放大倍率 * M放大倍率)
M = 放大倍率
WFN = 工作光圈数
P = 图元大小(微米)
K = 应用程式特定参数
应用程式特定参数取决於应用的类型。对於远心测量应用来说一个合理的应用程式特定参数值是0.015,而缺陷检测应用程式特定参数应设置约0.008 。对於一定的放大倍率和工作光圈数,因为双面聚焦远心,我们镜头的景深是更好的
下面我们以计算双远心镜头2364景深为例子,来说明远心镜头景深计算公式:
以下为双远心镜头2364产品目录资料:
M=放大倍率=0.38
P=图元大小=4.4um (根据你所采用相机而定)
K=0.015(应用程式特定参数)
F/N = 光圈数=8
WFN=工作光圈数== (1+放大倍率)*焦距比数 = (1+ 0.138)*8 = 9.104
景深=(工作光圈数*图元大小*应用程式特定参数)/(放大倍率*放大倍率)= (9.104 * 4,4 * 0,015) / (0.138 * 0.138) = 31.55 mm
然而双远心镜头产品目录上的景深资料为35mm。
正如您所看到的,用公式得出的资料与我们实际产品册上面的资料略微有所不同,实际上我给到您的公式只是计算资料的一种方法(许多实际上的资料应用是无法依照公式来判断的).景深其实并不困难,所以如果您愿意的话,你们可以自己测量一下。
测量镜头的景深的方法如下:
1)把您的镜头与被测物的工作距离调到正确的位置;
2)一旦您的画面对焦,使用软体测量你的物体;
3)现在移动物体使之接近镜头然后远离镜头,看您的软体测量的结果;
4)你可以看到你的成像画面在允许范围里是不会改变的,这个范围就是我们所谓的景深范围。
畸变作为光学系统中经常提到的一个参数,是限制光学量测准确性的重要因素之一。它是光学系统对物体所成的像相对於物体本身而言的失真程度,只引起像的变形,对像的清晰度并无影响。
对於理想光学系统,在一对共轭的物像平面上,放大率是常数。但是对於实际的光学系统,仅当视场较小时具有这一性质,而当视场较大或很大时,像的放大率就要随视场而异,这样就会使像相对於物体失去相似性。这种使像变形的成像缺陷称为畸变。
畸变定义为实际像高与理想像高差,而在实际应用中经常将其与理想像高之比的百分数来表示畸变,称为相对畸变,即
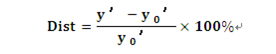
有畸变的光学系统,若对等间距的同心圆物面成像,其像将是非等间距的同心圆。当系统具有正畸变时,实际像高随视场的增大比理想像高增大得快,即放大倍率随视场的增大而增大,则同心圆的间距自内向外逐渐增大;反之,当为负畸变时,圆的间距自内向外逐渐减小。对於普通的光学镜头,只要感觉不出它所成像的变形,这种成像缺陷就可忽略;但是对於某些要利用像来测定物体大小尺寸的应用,畸变的影响就非常重要了,它直接影响测量精度。
普通工业镜头的畸变一般在1%~2%,这样的畸变通常会影响检测精度(例如实际长度为100mm的物体,使用这种镜头测得的尺寸可能是101mm~102mm;而我们ES远心光学的双远心镜头,畸变一般都小於0.1%,畸变系数为普通镜头的1/20,大大提高了检测精度和稳定性,达到了目前最高标准光学测试仪器的测量极限。
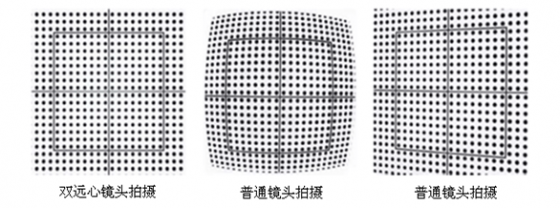
左图为双远心镜头拍摄的畸变测试图,完全无径向畸变或梯形畸变;中图为明显径向畸变;右图为明显梯形畸变。

