相關連結:http://www.esstartek.com/yellowpage/product_cg146475.html
StartFromHere

遠心鏡頭 設計目的就是消除由於被測物體(或CCD晶片)離鏡頭距離的遠近不
一致,造成放大倍率不一樣。根據遠心鏡頭分類其設計原理如下:
1.物方遠心光路設計原理及作用:
物方主光線平行於光軸主光線的會聚中心位於像方無限遠,稱之為:物方遠心光路。其作用為:可以消除物方由於調焦不準確帶來的,讀數誤差。
2.像方遠心光路設計原理及作用:
像方主光線平行於光軸主光線的會聚中心位於物方無限遠,稱之為:像方遠心光路。其作用為:可以消除像方調焦不准引入的測量誤差。
3.兩側遠心光路設計原理及作用:
綜合了物方/像方遠心的雙重作用。主要用於視覺測量檢測領域。
從以上各類遠心鏡頭設計原理即可看出,遠心鏡頭是在充分利用光學成像特性,充分考慮在成像中光線的影響而設計的高精度鏡頭,目前在機器視覺精密測量、高精度檢測領域已被廣泛應用。
EndAtHere
遠心光學系統公司(ES)是一家專業的遠心光學、視覺照明、機電產品研究、設計、開發、製造的高科技企業。滿足客戶對特殊規格和特性的需求,公司可量身為您定制遠心光學鏡頭、視覺照明、遠心光學系統設備平臺等軟硬體,並為您提供一站式技術顧問服務,使您更簡單、更快速地建立自己的自動化遠心視覺應用系統。
在產品選型中,有的朋友對於光學的專業術語或多或少會有一些疑問,今天,小編為您答疑解惑悉數奉上。
一、數值孔徑N.A.:
當物件的入射光瞳時半形是u,而折射率是n,n*sin u是物體方數值孔徑N.A.;
當物件的出射光瞳時半形是u',而折射率是n',n'*sin u'是物體方數值孔徑N.A.;
數值孔徑是一個度量鏡頭解析度及光亮度的重要指標,N.A.數值越高,解析度及光亮度越高。
二、解析度:
能清楚區分被測物體細微結構最小間隔的能力。即,能清楚區分相鄰兩個物點間最小距離的能力。解析度越大,兩點之間可區分的最小距離越小。數值孔徑越大,解析度越高。
解析度公式:解析度(ε)=0.61×λ/N.A.
λ:使用的波長或輻射(λ=0.55um用於可見光)
N.A.:物鏡數值孔徑
三、景深:
景深是指無需重新調焦即可保持可接受的圖像清晰度的距離。
景深計算公式:
景深=2×(允許彌散圓×有效Fno/放大倍率2)=允許彌散圓/(N.A.×放大倍率)
(注:有效Fno=放大倍率/2N.A.)
四、F數/光圈數:
<顯示了光亮度,計算方式是鏡頭焦距除以從鏡頭的物體測觀測到有效直徑(入射光瞳D mm)。它可以用N.A.及鏡頭的光學放大率(β)計算出來。Fno=f/D= β/(2×N.A.)。
五、有效F數/有效光圈:
有效F數顯示了物體在有限距離的鏡頭光亮度。用來表示實際使用的鏡頭的光亮度數值,光學放大率越高,鏡頭越暗。有效Fno=(1+β)×Fno。
六、放大倍率:
電子放大倍率:用相機拍照成像呈現在顯示器的放大倍率。
光學放大倍率(β):影像大小相對於物體的放大倍率。
β=影像/物體=N.A./N.A.'=CCD相機靶面尺寸/視場實際尺寸
有效F數顯示了物體在有限距離的鏡頭光亮度。用來表示實際使用的鏡頭的光亮度數值,光學放大率越高,鏡頭越暗。有效Fno=(1+β)×Fno。
七、視場:
視場是鏡頭與CCD相機連接時物體可被看見的範圍大小。
視場大小=(CCD靶面大小)/(光學放大倍率)。
八、焦距/後焦點/前焦點:
焦距:光學系統中心到焦點的距離;
後焦點:最後一片鏡片到後側焦點的距離;
前焦點:最前一片鏡片到前側焦點的距離。
遠心光學(ES)核心技術人員在航太、軍工領域從事光學設計、製造工作10多年,積累和掌握了一系列先進的遠心光學、光機及視覺照明技術、製造工藝及嚴謹的測試流程。產品精良,在行業應用中獲得諸多好評,有相關的行業知識您都可以在網站的技術資料中查閱。
在計量學應用中進行精密線性測量時,經常需要從物體標準正面觀測,此外,許多機械零件並無法精確放置,測量時間距也在不斷變化,而軟體工程師卻需要能夠精確反映實物的圖像。這就需要用遠心鏡頭來完成--高遠心度、無透視誤差。
遠心度是描述主光線偏離於光軸的角度,角度越小遠心度越好,成像就越精確。一個理想的遠心鏡頭沒有梯形畸變,遠心度是0°。
對於很多應用需要用到遠心鏡頭是因為遠心鏡頭在很大工作距離內的放大倍率接近恒定,消除了視角誤差。這就意味著物體運動不會影響像的放大倍率。
需要注意地是:並不是遠心鏡頭就比普通鏡頭有更大的景深。事實上,遠心度高並不意味著景深大,景深僅僅依賴於F-number和解析度。使用遠心鏡頭,隨著物體遠離最佳焦距成像也會模糊,但是它是對稱模糊(這已被當作遠心鏡頭的優點)。

普通鏡頭拍攝 雙遠心鏡頭拍攝
只要物體的特徵在遠心鏡頭工作距離內,像的放大倍率保持恒定,換言之,即離透鏡近的特徵並不比離的遠的成像大。比如需要同時檢測相隔10mm的兩個相同螺絲的螺紋分佈。
左圖是普通鏡頭拍攝的,存在視角誤差,放大倍率不一致;右圖是我們ES Star的雙遠心鏡頭ESCM125-80-AL搭配遠心光源拍攝,全視場無視差,拍攝畫面很完美。
解析度(resolution)又稱分辨力、鑒別率、鑒別力、分析力、解像力和分辨本領,是指攝影鏡頭清晰地再現被攝景物纖微細節的能力,是評價鏡頭品質的一個重要參數。顯然解析度越高的鏡頭,所拍攝的影像越清晰細膩。它的優點是可以量化,用資料表示(圖像解析度一般以量化圖像感測器即空間頻率對比度CTF(對比傳遞函數)來衡量),使結果更直觀、更科學、更嚴密。
解析度定義為在像面處鏡頭在單位毫米內能夠分辨開的黑白相間的條紋對數,如下圖所示:

解析度為1/2d,其中,d為線寬。解析度的單位為lp/mm(線對/毫米)。
一般使用的解析度公式:
解析度(ε)=0.61×λ/N.A.(Reyleigh公式)
λ:使用的波長或輻射(λ=0.55µm用於可見光)
N.A.:物鏡數值孔徑
在實際工業應用中,系統使用面陣或線陣感測器作為成像器件,因此系統的解析度通常也會受到成像感測器中像元解析度的限制。像元解析度定義為單位毫米內圖元單元數的一半,即=1/2P,其中p為圖元單元的尺寸大小。例如一個CCD的像元尺寸大小為5×5微米,則像元解析度則為:=1/(2*0.005)=100(lp/mm)。感測器的像元解析度限制了系統的最高解析度,即使鏡頭的解析度再高,系統也不可能分辨高於像元解析度的細節。
在實際使用中,普通鏡頭解析度低,即使搭配高圖元的相機,最後也只能生成模糊的影像。而採用我們BTOS遠心光學公司的鏡頭,即使是配合小圖元圖像感測器,也能生成高解析度圖像。

ES 遠心鏡頭 普通鏡頭
景深,在光學攝影中是一個很重要參數,它的大小決定著清晰圖像範圍。在遠心光學成像中,景深也是一個經常被提及的參數,它的大小取決於鏡頭倍率、光圈數、波長、圖元大小、客戶使用的邊緣提取演算法靈敏度。對於大多數遠心系列鏡頭,陳述的景深是在光圈數為8的整體景深。景深可用于測量應用,它通常比缺陷檢測景深要大,圖像的對比度必須盡可能高。
由於這個原因,遠心光學系統(ES Stacy)公司的產品記錄指出,"景深邊界,圖像可仍用於測量,但為了得到一個非常清晰的圖像,應考慮只有一半的名義景深"。景深非常困難用參數來定義:它取決於倍率、光圈數、波長、圖元大小、客戶使用的邊緣提取演算法的靈敏度。由於這個原因:沒有客觀的,也沒有標準的方式來定義它:這是一個主觀參數。
一個簡單的法則,快速計算景深的方法如下:
景深 = (工作光圈數 * 圖元大小 * 應用程式特定參數) / (放大倍率 * M放大倍率)
M = 放大倍率
WFN = 工作光圈數
P = 圖元大小(微米)
K = 應用程式特定參數
應用程式特定參數取決於應用的類型。對於遠心測量應用來說一個合理的應用程式特定參數值是0.015,而缺陷檢測應用程式特定參數應設置約0.008 。對於一定的放大倍率和工作光圈數,因為雙面聚焦遠心,我們鏡頭的景深是更好的
下面我們以計算雙遠心鏡頭2364景深為例子,來說明遠心鏡頭景深計算公式:
以下為雙遠心鏡頭2364產品目錄資料:
M=放大倍率=0.38
P=圖元大小=4.4um (根據你所採用相機而定)
K=0.015(應用程式特定參數)
F/N = 光圈數=8
WFN=工作光圈數== (1+放大倍率)*焦距比數 = (1+ 0.138)*8 = 9.104
景深=(工作光圈數*圖元大小*應用程式特定參數)/(放大倍率*放大倍率)= (9.104 * 4,4 * 0,015) / (0.138 * 0.138) = 31.55 mm
然而雙遠心鏡頭產品目錄上的景深資料為35mm。
正如您所看到的,用公式得出的資料與我們實際產品冊上面的資料略微有所不同,實際上我給到您的公式只是計算資料的一種方法(許多實際上的資料應用是無法依照公式來判斷的).景深其實並不困難,所以如果您願意的話,你們可以自己測量一下。
測量鏡頭的景深的方法如下:
1)把您的鏡頭與被測物的工作距離調到正確的位置;
2)一旦您的畫面對焦,使用軟體測量你的物體;
3)現在移動物體使之接近鏡頭然後遠離鏡頭,看您的軟體測量的結果;
4)你可以看到你的成像畫面在允許範圍裡是不會改變的,這個範圍就是我們所謂的景深範圍。
畸變作為光學系統中經常提到的一個參數,是限制光學量測準確性的重要因素之一。它是光學系統對物體所成的像相對於物體本身而言的失真程度,只引起像的變形,對像的清晰度並無影響。
對於理想光學系統,在一對共軛的物像平面上,放大率是常數。但是對於實際的光學系統,僅當視場較小時具有這一性質,而當視場較大或很大時,像的放大率就要隨視場而異,這樣就會使像相對於物體失去相似性。這種使像變形的成像缺陷稱為畸變。
畸變定義為實際像高與理想像高差,而在實際應用中經常將其與理想像高之比的百分數來表示畸變,稱為相對畸變,即
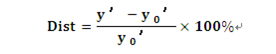
有畸變的光學系統,若對等間距的同心圓物面成像,其像將是非等間距的同心圓。當系統具有正畸變時,實際像高隨視場的增大比理想像高增大得快,即放大倍率隨視場的增大而增大,則同心圓的間距自內向外逐漸增大;反之,當為負畸變時,圓的間距自內向外逐漸減小。對於普通的光學鏡頭,只要感覺不出它所成像的變形,這種成像缺陷就可忽略;但是對於某些要利用像來測定物體大小尺寸的應用,畸變的影響就非常重要了,它直接影響測量精度。
普通工業鏡頭的畸變一般在1%~2%,這樣的畸變通常會影響檢測精度(例如實際長度為100mm的物體,使用這種鏡頭測得的尺寸可能是101mm~102mm;而我們ES遠心光學的雙遠心鏡頭,畸變一般都小於0.1%,畸變係數為普通鏡頭的1/20,大大提高了檢測精度和穩定性,達到了目前最高標準光學測試儀器的測量極限。
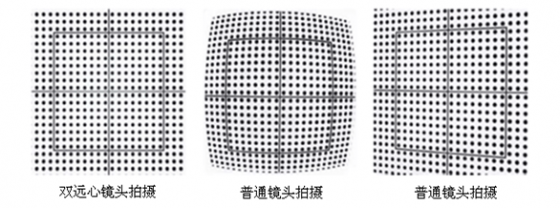
左圖為雙遠心鏡頭拍攝的畸變測試圖,完全無徑向畸變或梯形畸變;中圖為明顯徑向畸變;右圖為明顯梯形畸變。

